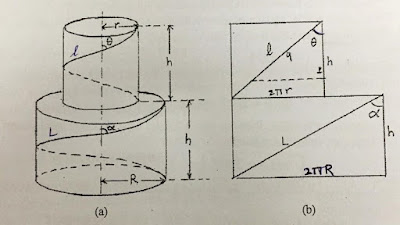
Assumptions:
1. Yarn cross-section is circular.
2. The fibres follow the helical curves on the nested concentric cylinder.
3. The fibre on the yarn axis is straight, or linear, and the Helix angle and Helix diameter of the fibres increase as they move away from the yarn axis and reach the maximum value on the yarn surface.
4. Twist along the yarn remains constant in all yarn layers.
5. The packing density of the fibres in the yarn structure is constant everywhere.
6. Yarn cross-section consists of a large number of fibres.
Notations:
R: radius of yarn
r: radius of the cylinder containing the helical path of a particular fibre
T: Yarn twist
h: length of one turn of twist
α: twist angle at the surface
θ: twist angle at the helical cylinder
l: length of fibre in one turn of twist on the helical cylinder
L: length of fibre in one turn of twist at the surface.
From the above figure:
Now from equation (3) and (4):
On the other hand, as shown in Figure (b), the length of fiber, q measured along the helix with radius r located at any length of thread, z:
Now putting the value of θ from equation (5),
Again, if T is the number of twists in the unit length of yarn:
and
The following equation of yarn diameter and twist has been found from surface twist angle and basic parameters of yarn:
Texpedi.com
